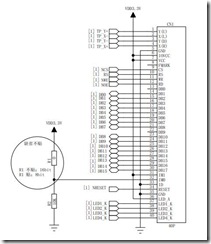
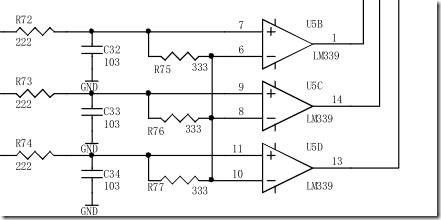
无感无刷电机使用FOC驱动时，需要通过反电动势计算转子电角度

θ = arctan (-e α , e β )

如果使用math.h的atan()函数，计算量大，耗时长，FOC每次中断间隔是PWM的周期，在PWM频率为16K时，62.5us中断一次，所以要求反正切计算时间尽量短。使用CORDIC算法会明显加快计算速度。

CORDIC算法的思路很简单，在坐标系中，将（x,y）旋转一定的角度，如果旋转之后y=0,那么旋转的角度就是我们要求解的反正切角θ。但是我们事先并不知道要旋转多少角度才能让旋转之后的纵坐标y=0，因此，我们每次旋转某一固定角度，每次旋转角度都为前一次旋转角度的一半，并且需要根据纵坐标y的数值正负进行旋转方向的选取，如此经过多次旋转之后，就能让y趋近于0，而每次旋转的角度累加出来的结果就是我们要求取的反正切角θ。

X,y平面坐标有两个点P,Q, Q由P逆时针旋转θ得到。

PQ两点的坐标为

Xp=cosα

Yp=sinα

Xq=cos(α+θ)=cosαcosθ-sinαsinθ=xp*cosθ-yp*sinθ

Yq=sin(α+θ)=sinαcosθ+sinθcosα=yp*cosθ+xp*sinθ

Xq=cosθ(cosα-sinαtanθ)= cosθ(cosα-yp*tanθ)

Yq=cosθ(sinα+tanθcosα)= cosθ(sinα+xp*tanθ)

把cosθ去掉得到

Xq=cosθ(cosα-sinαtanθ)= xp-yp*tanθ

Yq=cosθ(sinα+tanθcosα)= yp+xp*tanθ

去掉cosθ后，旋转的角度仍然是正确的，因为cosθ在0-1之间，模值变大了

现在求反正切角α，开始旋转，旋转的目标是yq=0。每次旋转固定的角度，每次旋转的角度逐渐减小，并且考虑旋转方向，这样经过迭代，最终能使Q点在x轴上。然后把每次旋转的角度累加，就得到要求的反正切角了。那么每次旋转多少角度呢？把等式中的tanθ换成，每次旋转atan()角度，i表示第几次旋转，这样上面的式子就变成了

Xq= xp-yp*，

Yq= yp+xp*，

例如第一次旋转i=0,旋转角度为atan(1),即45度，第二次旋转i=1,旋转角度为atan(1/2),即26.5650度，这样我们能够把乘法运算变为移位运算，大大提高运算效率。

如果我们把上面16次的角度都累加起来，用这个方法能求的角度范围在[-99.8829°,99.8829°]，所以在这个角度内都可以旋转，如果是在二三象限的矢量，则需要，先旋转90度，到一四象限。然后再迭代。

把旋转方向考虑进来

X(i+1)=x(i)-d(i))

y(i+1)=y(i)+d(i))

z(i+1)=z(i)-d(i) *θ(i)

式中d(i)用于确定旋转的方向，顺时针为-1，逆时针为1.

以求30度反正切角为例

根据z(i+1)=z(i)-d(i) *θ(i)

旋转角度=45-26.565+14.036……-0.004-0.002=29.999

注意d(i)符号。

C语言实现：

u16 AngleTab[] ={0x2000,0x12E4,0x09FB,0x0511,0x028B,0x0146,0x00A3,0x0051,0x0029,0x0014,0x000A,0x0005,0x0003,0x0001,0x0001,0x0000};

定义16个旋转角度值，FOC角度范围为-32768-32767

0x2000对应45度，0x12e4对应26.565度…

实现函数如下：

首先把角度转换到第一象限的[0°,45°]范围内。计算出反正切角后，再转到-32768-32767范围内。